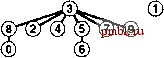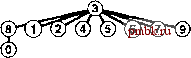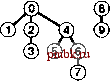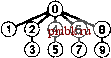решение очень сложных встречающихся на практике задач за приемлемое время (см. упражнение ].]]). Ценой добавления нескольких дополнительных строк кода мы получаем программу, которая при решении очень сложных задач, которые могут встретиться на практике, работает буквально в миллионы раз быстрее, чем более простые алгоритмы.

Из приведенных схем .видно, что лишь сравнительно небольшое количество узлов располагаются далеко от корня; действительно, экспериментальное изучение очень сложных задач показывает, что как правило, для решения практических задач посредством использования алгоритма взвешенного быстрого объединения, реализованного в программе 1.3, требуется линейное время. То есть затраты времени на выполнение алгоритма связаны с затратами времени на считывание ввода постоянным коэффициентом. Вряд ли можно было бы рассчитывать найти более эффективный алгоритм.

Немедленно возникает вопрос, можно ли найти алгоритм, обеспечивающий гарантированную линейную производительность. Этот вопрос - исключительно трудный, который уже много лет не дает покоя исследователям (см. раздел 2.7). Существует множество способов дальнейшего совершенствования алгоритма взвешенного быстрого объединения. В идеале было бы желательно, чтобы каждый узел указывал непосредственно на корень своего дерева, но за это не хотелось бы расплачиваться изменением большого количества указателей, как это делалось в случае алгоритма быстрого объединения. К идеалу можно приблизиться, просто делая все проверяемые узлы указывающими на корень. На первый взгляд этот шаг кажется весьма радикальным, но его легко реализовать, а в структуре этих деревьев нет ничего неприкосновенного: если их можно изменить, чтобы сделать алгоритм более эффективным, это следует сделать. Этот метод, названный сжатием пути (path compression), можно легко реализовать, добавляя еще один проход по каждому пути во время выполнения операции union и устанавливая запись id, соответствующую каждой встреченной вершине, указывающей на корень. В результате деревья становятся почти совершенно плоски-

РИСУНОК 1.9 СЖАТИЕ ПУТИ

Пути в деревьях можно сделать еще короче, просто делая все просматриваемые объекты указывающими на корень нового дерева для операции объединения, как показано в этих двух примерах. В примере на верхнем рисунке показан результат, соответствующий рис.

1.7. В случае коротких путей сжатие пути не оказывает никакого влияния, но при обработке пары 1 6, мы делаем узлы 1, 5 и 6 указывающими на узел 3, в результате чего дерево становится более плоским, чем на рис 1.7 В примере на нижнем рисунке показан результат, соответствующий рис.

1.8. В деревьях могут появляться пути, которые содержат больше одной-двух связей, но при каждом их прохождении мы делаем их более плоскими. В данном случае при обработке пары б 8 мы делаем дерево более плоским, делаяуз.ш 4, 6и 8 указывающими на узел 0.

ми, приближаясь к идеалу, обеспечиваемому алгоритмом быстрого поиска, как показано на рис. 1.9. Анализ, устанавливающий этот факт, исключительно сложен, но сам метод прост и эффективен. Результат сжатия пути для большого примера показан на рис. Ы1.

Существует множество других способов реализации сжатия пути. Например, программа 1.4 - реализация, которая сжимает пути, делая каждую связь перескакивающей к следующему узлу в пути вверх по дереву (см. рис. 1.10). Этот метод несколько проще реализовать, чем полное сжатие пути (см. упражнение 1.16), но он дает тот же конечный результат. Мы называем этот вариант взвешенным быстрым объединением посредством сжатия пути делением пополам (weighted quick-union with path compression by halving). Какой из этих методов эффективнее? Оправдывает ли достигаемая экономия время, требующееся для реализации сжатия пути? Существует ли какая-либо иная технология, применение которой следовало бы рассмотреть? Чтобы ответить на эти вопросы, следует внимательнее присмотреться к алгоритмам и реализациям. Мы вернемся к этой теме в главе 2 в контексте рассмотрения основных подходов к анализам алгоритмов.

Программа 1.4 Сжатие пути делением пополам

Если циклы for в программе 1.3 заменить этим кодом, длина любого проходимого пути будет делиться пополам. Конечный результат этого изменения - превращение деревьев в почти совершенно плоские после выполнения длинной последовательности операций.

for (i = р; i != id[i3; i = id[i3)

id[i] = id[id[i3];

for (j = q; j != id[j3 ; j = id[j])

id[j] = id[id[j]3;

Ф (8)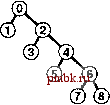

РИСУНОК 1.10 СЖАТИЕ ПУТИ ДЕЛЕНИЕМ ПОПОЛАМ

Можно уменьшить длину путей вверх по дереву почти вдвое, прослеживая две связи одновременно и устанавливая нижнюю из них указывающей на тот же узел, что и верхняя, как показано в этом примере. Конечный результат выполнения такой операции для каждого проходимого пути приближается к результату, получаемому в результате полного сжатия пути.

РИСУНОК 1.11 БОЛЬШОЙ ПРИМЕР ВЛИЯНИЯ СЖАТИЯ ПУТИ

Здесь отображен результат обработки случайных пар 100 объектов алгоритмом взвешенного быстрого объединения с сжатием пути. Все узлы этого дерева, за исключением двух, находятся на расстоянии одного-двух шагов от корня.

Конечный результат применения рассмотренных алгоритмов решения задачи связности приближается к наилучшему, на который можно было бы рассчитывать в любом практическом случае. Мы имеем алгоритмы, которые легко реализовать и время выполнения которых гарантировано связано с затратами времени на сбор данных постоянным коэффициентом. Более того, алгоритмы являются оперативными, рассматривающими каждое ребро только один раз и использующими объем памяти, который пропорционален количеству объектов; поэтому какие-либо ограничения на количество обрабатываемых ими ребер отсутствуют. Результаты экспериментального исследования, приведенные в табл. 1.1, подтверждают вывод, что программа 1.3 и ее варианты с использованием сжатия пути полезны даже в очень больших практических приложениях. Выбор лучшего из этих алгоритмов требует тщательного и сложного анализа (см. главу 2).

Таблица 1.1. Результаты экспериментального исследования

алгоритмов объединения-поиска

Эти сравнительные значения времени, затрачиваемого на решение случайных задач связности с использованием алгоритмов объединения-поиска, демонстрируют эффективность взвешенной версии алгоритма быстрого объединения. Дополнительный выигрыш благодаря использованию сжатия пути менее очевиден. Здесь М - количество случайных соединений, генерируемых до тех пор, пока все N объектов не оказываются связанными. Этот процесс требует значительно больше операций find, чем операций union, поэтому быстрое объединение выполняется существенно медленнее быстрого поиска. Ни быстрый поиск, ни быстрое объединение не годятся для случая, когда значение N очень велико. Время выполнения при использовании взвешенных методов явно пропорционально значению N, поскольку оно уменьшается вдвое при уменьшении N вдвое.

Ключ: F

быстрый поиск (программа 1.1)

быстрое объединение (программа 1.2)

взвешенное быстрое объединение (программа 1.3)

взвешенное быстрое объединение с сжатием пути (упражнение 1.16)

взвешенное быстрое объединение с делением пополам (программа 1.4)